---

We live in a three-dimensional world, and we perceive our world in 3D. It is our brains that construct our world to be seen in 3D.

In mathematics, we know that a 2D plane has two perpendicular directions x, y in a cartesian coordinate system. In the third dimension, the z axis is perpendicular to both x, y dimensions.

Similarly, the fourth dimension is a direction w perpendicular to all three x, y, z dimensions. This is hard for us to understand because we cannot visualize the fourth dimension, but we can deduce some interesting properties by walking our way up from lower dimensions. Although we can explain higher dimensions with mathematics, I will try to keep things simple in this post.

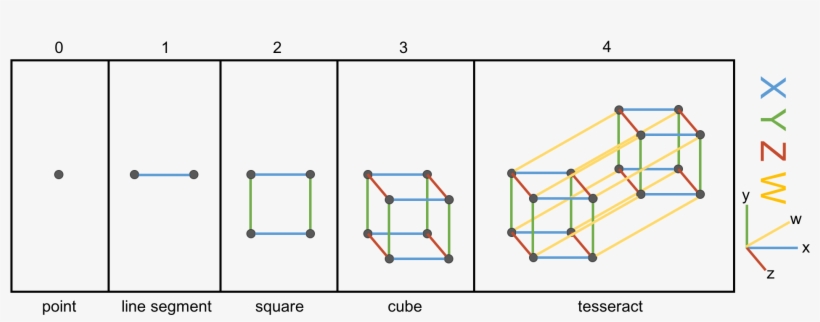
Lets start from 0D and walk our way up to 4D.

0D – the zeroth dimension

The zeroth dimension is a point. It has no dimensions; no width, no length, and no height.

1D – the first dimension

The first dimension is a line. The only thing that differs between objects in 1D are the differences in their length.

2D – the second dimension

A line extruded perpendicular to the first dimensional direction brings you to the second dimension. 2D objects have a length and width. A line moved perpendicular by the same length will make up a square.

• A square has 4 lines.

3D – the third dimension

The square extruded perpendicular to the 2D plane will make up a cube. In other words, extruding the square to the z axis makes up a 3D cube.

It is interesting to note that when a cube is expanded to infinity, it encompasses the entirety of the 3-dimensional space. A similar concept applies for other dimensions as well.

• A cube has 6 faces. Each face is a square.

We are all quite familiar with a drawing of a 3D cube on paper or on a computer screen. Really, this is how our brains are taught to understand a representation of the cube projected to 2D surface. What we are actually seeing is a shadow (or projection) of a wireframe cube cast on a 2D surface. Depending on the angle you look at it, the 2D projection will differ, but here is an angle we all are familiar with:

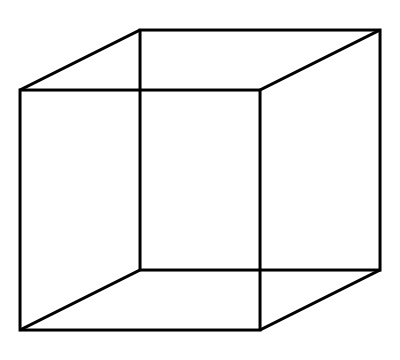
It is easier for our brain to decipher this 2D drawing as a cube when its rotating.

Extrapolating these concepts to the next dimension, we will be able to understand 4D objects and its behavior.

4D – the fourth dimension

A cube extruded perpendicular to the third dimension yields a tesseract (also called a hypercube). A tesseract is not an easy object we can easily comprehend, but it is the same as moving from 2D to 3D. We get a tesseract when a cube is protruded along the fourth dimension on the w axis.

Just like the square and cube, all edges in a tesseract are of the same length, and all angles are right angles.

• A tesseract has 8 cells. Each cell is a cube.

Just like the cube, we can cast a shadow of a tesseract on to a 2D surface. We will see different projections depending on the angle we look at.

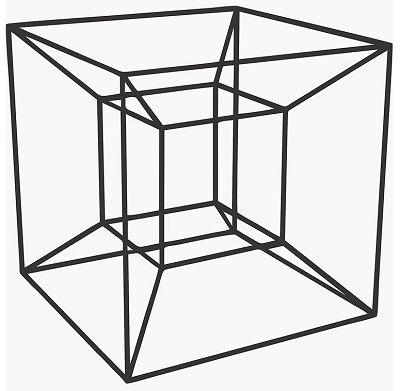
Just as the rotating cube, we would see a rotating tesseract like this:

This might not be intuitive as the rotating cube, and our brains have a hard time understanding 4D object like this. Just as you would see a square if you look directly at a face of a solid cube, you would see a cube if you look straight at a tesseract cell. You will see different perspectives of a tesseract when viewed from different angles.

Remember that this is not how a tesseract would actually look like. We are simply seeing a projection (or shadow) of a tesseract on a 2D surface. What you are seeing is a 4D object in a 3D world shown on a 2D screen! Far from what it really is.

If you are fascinated by the tesseract, you can now interact with this four-dimensional object in 3D space using virtual reality simulations. This is the closest we can get right now to a 4D object.

There are some interesting thought experiments about how we would perceive 4D objects entering our 3D world that we consider as our reality. The astrophysicist Carl Sagan explains nicely this in this classic video.